Designing against Deceit

Only a few months ago in a short manuscript detailing potential issues facing software engineers in the wake of ever-evolving AI systems, researchers Gros, Devanbu, and Yu described an impending reality where most computer code is written by machines [GDY 2023]. In such a reality, how can we guarantee that the code generated by these advanced machines be a safe and honest attempt aligned to the prompter's intent?

Generative models are impressive at producing code. As explained by Ajeya Cotra of Open Philosophy, experts' prediction back in 2016 of a computer being able to implement a standard algorithm like quicksort no sooner than within a decade was accomplished as early as 2021, and since shattered by the sophisticated coding capabilities of the language models of 2022 [Cotra 2023]. Naturally, access to these tools has impacted every programmer: a 2022 report by Google Research showed that over 3% of new internal code to Google was written by a generative AI autocomplete system only deployed 3 months prior [MS 2022]. With the widespread awakening to and adoption of generative language tools within (and beyond) software engineering, one can only imagine that this figure has since grown substantially. Developers' time is shifting from implementation to more abstract activities focused on design, testing, and review.

Before we fully pass off the buck of producing code to machines, we should step back to wonder how we might trust their outputs. Gros et. al illustrate this issue with an example:

This idea of verifiable code is not new: historically, George Necula might be credited with its advent. In his 1997 Proof-Carrying Code, Necula addressed the situation in which an untrustworthy source provides computer code to be run by the recipient, offering a protocol for guaranteeing that the received code adhere to certain, specified safety properties [Necula 1997].

Loosely, proof-carrying codes should be thought of as a pair of outputs: one part being the code generated by the source, and the other part a demonstration that the code meets some pre-defined safety criteria. This demonstration will be in the form of a binary string which the recipient would run through a formal theorem checker to ensure the provided code corresponds to this proof and satisfies the criteria. This setup requires that the source not only be capable of producing the desired code, but also generating the verifiable proof string. See the figure below for a pictorial representation of this scheme.

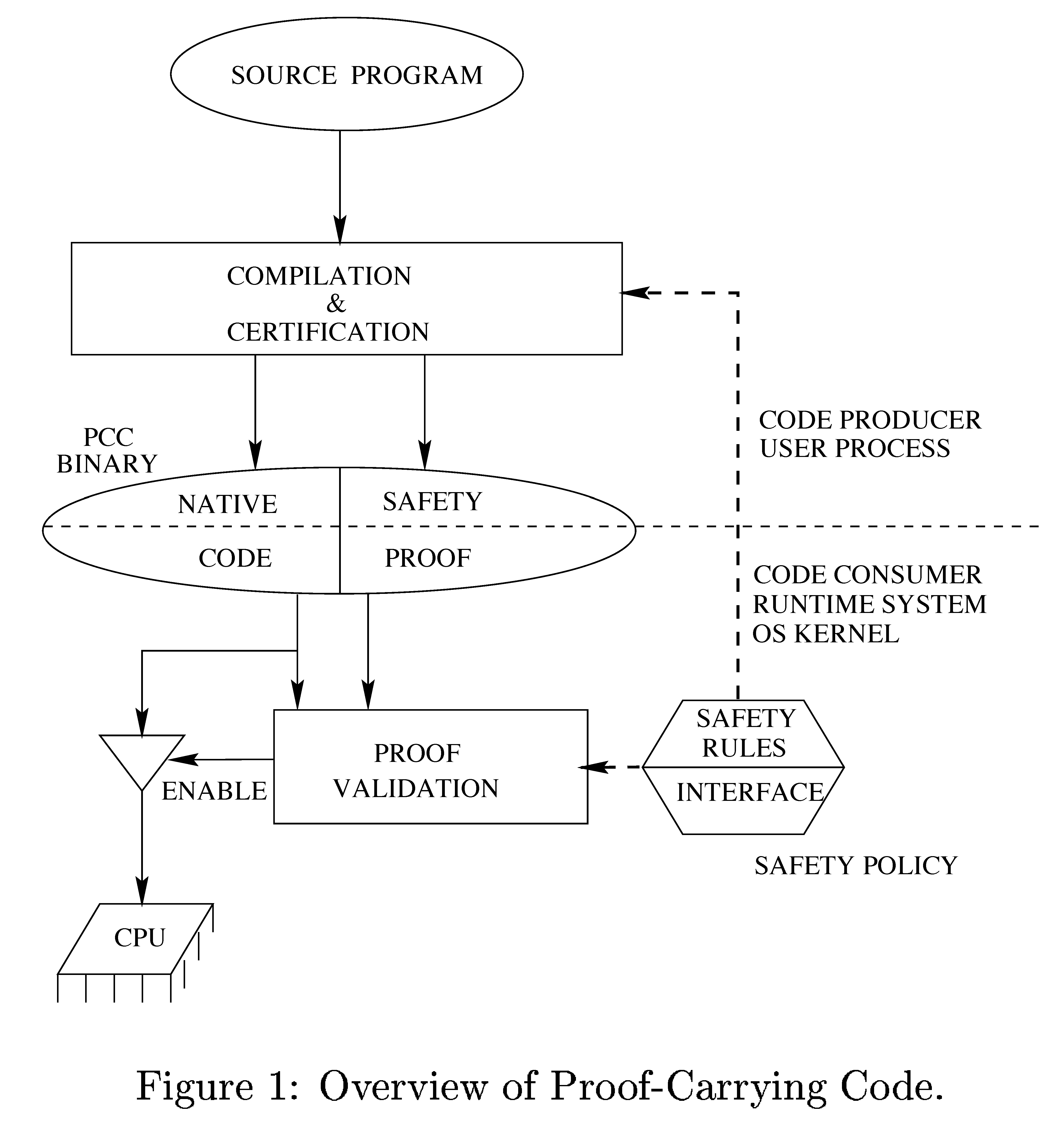
Necula originally regarded his work as a means to

1. Ensure that programs written in less readable assembly language be just as safe to share and execute as those in high-level language,
2. Surveil such assembly programs just as strictly as those in the strongly-typed, statically checked Meta-Language languages, and
3. Better manage both distributed and web computing.

Yet, we may easily reinterpret his work as a safety mechanism for executing any code received from an AI model.

In making the case for the necessity of proof-carrying codes, Necula argues that the cryptographic approach of establishing a "trusted party" from whom any code received should be automatically trusted is weak in the sense that it appeals to an authority which will always be fallible [Necula 1997]. The situation is even worse in the recent context of AI systems: we cannot guarantee the motives and performances of these models, so there is no real hope to follow the classical cryptographic approach for sharing code.

This basic concept has flourished over the past few decades, inspiring much more complicated schemes for trustworthy exchanges between the code producer and consumer. Software companies now formally verify that their source codes perform as advertised, app stores ensure the integrity of mobile applications before their deployment, programming languages might ensure type correctness and memory respect for source code and submitted libraries, and smart contracts that control blockchain networks are verified similarly. Gros et al. argue that protocols akin to Necula's proof-carrying code could be implemented, say, in systems running software interspersed with AI-generated code, serving as a proxy for control of the AI's outputs [GDY 2023].

Speculatively, the formal verifiability guaranteed by proof theory seems like a powerful approach to AI safety. We may be long off from a formal way to verify or even understand the features which emerge in trained models (see my post on Interpretability), but imposing the burden of "proof-carry" on any received code from an external source at least guarantees that a malicious source cannot undermine stated safety policies when offering code snippets. That we can produce mathematically sound protocols for code certification (i.e., pairing generated code with a certificate of satisfaction) and code validation (i.e., formally validating that the received code satisfies the safety policies using its certificate) is a feat of proof theory, and implies an optimistic path forward for more trustworthy code assistance interactions.

Theorem Checkers

The following information includes background on theorem checkers, a key component to any protocol mimicking proof-carrying code.

Theorem checkers are automated machines which attempt to deduce whether a provided proof truly demonstrates a desired theorem according to some presupposed logic (i.e., system of deduction) and axioms (i.e., ground-truths). Common theorem checkers in academia and industry include Coq, Isabelle, ACL2, and Lean. In particular, Lean is both an open-source theorem checker (automated) and proof assistant (human-aided), taking the form of a programming language based on a higher-order typed lambda calculus and began in 2013 by Leonadro de Moura. Lean-verified software or hardware systems are high-assurance and certainly more reliable than systems without formal verification.

I single out Lean amongst the rest because it is one of the easiest with which to start out. I recommend checking out the Natural Number Game produced by Kevin Buzzard and Jon Eugster. The game challenges the user to learn the various commands available in the Lean 4 language to gradually derive the theorems of arithmetic. Lean serves as the user's proof assistant, enabling the user to both write and check mathematical proofs interactively. I have written a blog post specifically to help the curious reader begin this game.

I believe that formal certification and validation will be absolutely necessary for successfully interacting with AI systems. Theorem checkers are the theoretically-backed hardware which make this trustworthy interaction possible. Jeremy Avigad of Carnegie Mellon University points out that theorem checkers also open the possibility for AI systems to translate any learned mathematical reasoning into the more easily verified symbolic reasoning [Avigad 2023]. It is highly likely that AI systems will one day be able to come up with new theorems, prove them in both the "human way" and the formal way: i.e., via writing formal proofs verifiable by theorem checkers, including theorems which a human may never have been able to even state due to their complexity.

AI systems are expected to continually encroach on the language-heavy activities performed by humans, so it is imperative to design systems which promote trustworthy assistance and verifiable claims.

References

• [GDY 2023] AI Safety Subproblems for Software Engineering Researchers. David Gros, Prem Devanbu, and Zhou Yu. 2023.
• [Cotra 2023] Language models surprised us. Ajeya Cotra. 2023.
• [MS 2022] ML-enhanced code completion improves developer productivity. Maxim Tabachnyk and Stoyan Nikolov. 2022.
• [Necula 1997] Proof-Carrying Code. George C. Necula. 1997.
• [Avigad 2023] Is Mathematics Obsolete. Jeremy Avigad. 2023.